概念
区间类动态规划是线性动态规划的扩展,它在分阶段地划分问题时,与阶段中元素出现的顺序和由前一阶段的哪些元素合并而来由很大的关系。令状态 $ f(i,j) $ 表示将下标位置 到 的所有元素合并能获得的价值的最大值,那么 $ f(i,j)=max{f(i,k)+f(k+1,j)+cost} $ ,$ cost $ 为将这两组元素合并起来的代价。
特点
合并 :即将两个或多个部分进行整合,当然也可以反过来;
特征 :能将问题分解为能两两合并的形式;
求解 :对整个问题设最优值,枚举合并点,将问题分解为左右两个部分,最后合并两个部分的最优值得到原问题的最优值。
练习题
石子合并1
石子合并1
分析
区间DP板题,使用前缀和进行优化,可通过下图进行理解
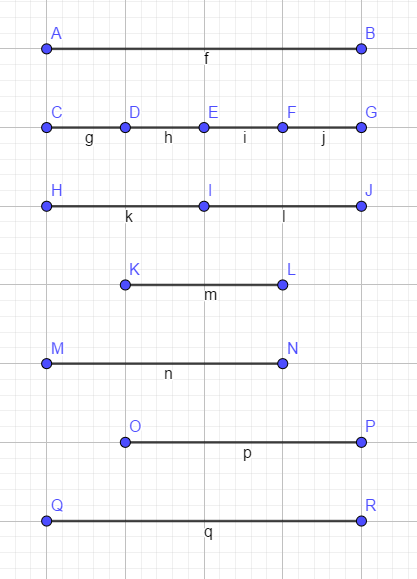
在此图中,g,h,i,j为题目所给的每堆的重量,k,l,m为长度为二时的最优策略…
如果要求区间k的值,则可以通过区间g和h求出,而点D则为分割点,其它线段以此类推,需要枚举的是分割点,以此最终求出答案
AC代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| #include <cstdio>
#include <cstring>
#include <algorithm>
const int MAXN = 105;
int n, m[MAXN][MAXN], a[MAXN], s[MAXN] = {};
int qujianhe(int start, int end) { return s[end] - s[start - 1]; }
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
s[i] = s[i - 1] + a[i];
}
for (int len = 2; len <= n; len++) {
for (int i = 1; i <= n - len + 1; i++) {
m[i][i + len - 1] = 0x3f3f3f;
for (int j = i; j < i + len - 1; j++) {
m[i][i + len - 1] = std::min(m[i][i + len - 1], m[i][j] + m[j + 1][i + len - 1] + qujianhe(i, i + len - 1));
}
}
}
printf("%d", m[1][n]);
return 0;
}
|
最长回文串
最长回文串
分析

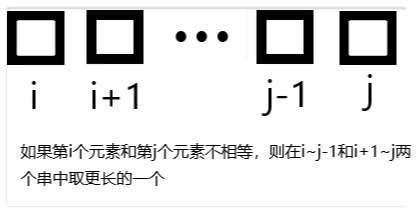
AC代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| #include <cstdio>
#include <cstring>
#include <algorithm>
const int MAXN = 3005;
int strl, f[MAXN][MAXN];
char str[MAXN];
int main() {
scanf("%s", str);
strl = strlen(str);
for (int i = 0; i < strl; i++) {
f[i][i] = 1;
}
for (int len = 2; len <= strl; len++) {
for (int i = 0; i <= strl - len; i++) {
if (str[i] == str[i + len - 1]) {
if (f[i + 1][i + len - 2] == len - 2) {
f[i][i + len - 1] = len;
} else {
f[i][i + len - 1] = std::max(f[i + 1][i + len - 1], f[i][i + len - 2]);
}
} else {
f[i][i + len - 1] = std::max(f[i + 1][i + len - 1], f[i][i + len - 2]);
}
}
}
printf("%d", f[0][strl - 1]);
return 0;
}
|
